Programming a Ballistic Calculator
Recap
In the last article, we reviewed Python fundamentals. We focused on:
- Variables
- Lists
- If statements
- For loops
These are the key pieces of knowledge we need to finally piece all the information together into a working ballistic calculator.
Programming a Ballistic Calculator
Now that we have Python installed and we have reviewed some programming fundamentals, we can start planning how we will program the ballistic calculator.
The first step is compiling all the information we will need to create the calculator. Starting with the equations of motion:
For x-direction:
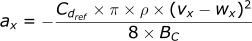
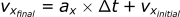
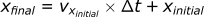
For y-direction:
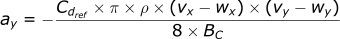
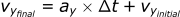
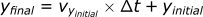
For z-direction:
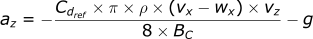
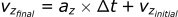
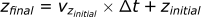
We will need the following inputs:
- tdelta
- Air density (ρ)
- Ballistic coefficient
- Cd reference table
- Muzzle velocity
- Rifle elevation angle when fired
- Wind velocity
The next step is to outline the process of calculations. We know from the example in the earlier section how to manually calculate the steps, how can we program this so that the computer will do the steps for us?
The process will look like this:
- Calculator inputs
- Determine initial vx and vz components of muzzle velocity
- Determine initial vx and vy components of wind velocity
- Run the acceleration, velocity, and position calculations in a loop until the bullet hits the ground
- Graph the trajectory profile
From this point on, we will cover the code required and provide annotations at key points.
Let’s first define the scenario we want to calculate:
- A rifle is fired at an elevation angle of 0.1 degrees in the North direction
- Muzzle velocity is 900 m/s
- Air density is 1.203 kg/m³
- The bullets BC is 0.2 lb/in² (G7 reference)
- The wind velocity is 5 m/s
- The wind is blowing from the North West (θ = 45°)
Note: Computers typically use radians for angles instead of degrees. One circle has 360 degrees, one circle in radians is 2*PI. Therefore conversion is:
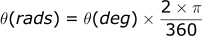
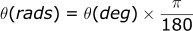
We will need to convert all of our input angles into radians for the computer to calculate the right answer.
The first thing we do is import the libraries we will be using for the program:
import matplotlib.pyplot as plt
import math
import csv
matplotlib is a charting library we installed earlier that will let us create the trajectory graphs. The math library is for the sin() and cos() functions we will need to use (this comes pre-installed with Python). The csv library will let us read the tables containing the reference drag coefficient values (pre-installed with Python).
We begin by setting our calculator inputs:
# Constants
pi = 3.14
g = 9.81
tdelta = 0.001
# Inputs
airDensity = 1.203
BC = 0.2
muzzleVelocity = 900
muzzleAngle = 0.1
windVelocity = 5
windAngle = 45
First we need to convert the BC into metric units (we covered this earlier):
BC = 703.7 * BC
We will then determine the initial conditions (xo, zo, yo, vxo, vzo, vyo):
muzzleAngle = muzzleAngle * pi / 180
windAngle = windAngle * pi / 180
xinitial = 0
vxinitial = muzzleVelocity * cos(muzzleAngle)
yinitial = 0
vyinitial = 0
zinitial = 0
vzinitial = muzzleVelocity * sin(muzzleAngle)
vtotal = muzzleVelocity
wx = windVelocity * -1 * cos(windAngle)
wy = windVelocity * -1 * sin(windAngle)
Now that we have the initial conditions, we need to tell the computer that we want it to do the same calculation over and over (like we did manually in the previous example). We can use a loop to make the computer repeat the same code, and use lists to keep track of all the values we calculate.
For the sake of demonstration, we will tell the computer to run the loop of code 1000 times.
First we need to create a place for the computer to store the values from these 1000 calculations. We do that by creating an empty Python list.
xList = []
vxList = []
axList = []
yList = []
vyList = []
ayList = []
zList = []
vzList = []
azList = []
Next we create a for loop and make it run 1000 times before it stops:
for i in range(0,1000):
# REST OF CODE
Before we go any farther, we will need to program the linear interpolation required to get the reference drag coefficient value at any velocity.
To program linear interpolation we will create a function to read the table of values from a spreadsheet (.csv file):
def dragCoefficient(v):
# We use 341.5 m/s as our conversion from m/s to mach speed
mach_conversion = 341.5
# Open up the csv file holding the table of reference Cd values
# IMPORTANT the file must be in the same location as this python script
# Change the "G7.csv " to the name of the csv file containing the data
with open("G7.csv") as G7DragFile:
# We create a list containing the rows from the table
G7Drag = list(csv.reader(G7DragFile))
# Interpolation (v - v1) / (v2 - v1) = (Cdref - Cdref1) / (Cdref2 - Cdref1)
# Cdref = (v - v1) / (v2 - v1) * (Cdref2 - Cdref1) + Cdref1
# The bottom index will keep track of the last row the computer looked at
bottom_index = 0
# The computer will need to check the velocity for each row of the table,
# until we find the two rows (v1 and v2) that are greater and less than v
for row in G7Drag:
# We use the float function to make sure that the computer recognizes
# the values in the table as numbers and not text
rowV = float(row[0]) * mach_conversion
# If v is equal to the current row velocity, we can return the Cd value
# directly from the table
if v - rowV == 0:
return row[1]
# If v is larger than the row velocity, we keep looking
elif v - rowV > 0:
bottom_index += 1
# If v is less than the current row, we know v is in between v1 and v2
elif v - rowV < 0:
# At this point, the bottom_index is at the current row (which is v2)
# so we set the top index as the row for v2 and Cdref2
top_index = bottom_index
# If we want the values for v1 and Cdref1,
# we need to get the row one before the current row.
v1 = float(G7Drag[bottom_index-1][0]) * mach_conversion
Cdref1 = float(G7Drag[bottom_index - 1][1])
# We then get the values for v2 and Cdref2
v2 = float(G7Drag[top_index][0]) * mach_conversion
Cdref2 = float(G7Drag[top_index][1])
# Using our linear interpolation formula
Cdref = (v - v1) / (v2 - v1) * (Cdref2 - Cdref1) + Cdref1
return Cdref
Our code now looks like this:
def dragCoefficient(v):
# We use 341.5 m/s as our conversion from m/s to mach speed
mach_conversion = 341.5
# Open up the csv file holding the table of reference Cd values
# IMPORTANT the file must be in the same location as this python script
# Change the "G7.csv " to the name of the csv file containing the data
with open("G7.csv") as G7DragFile:
# We create a list containing the rows from the table
G7Drag = list(csv.reader(G7DragFile))
# Interpolation (v - v1) / (v2 - v1) = (Cdref - Cdref1) / (Cdref2 - Cdref1)
# Cdref = (v - v1) / (v2 - v1) * (Cdref2 - Cdref1) + Cdref1
# The bottom index will keep track of the last row the computer looked at
bottom_index = 0
# The computer will need to check the velocity for each row of the table,
# until we find the two rows (v1 and v2) that are greater and less than v
for row in G7Drag:
# We use the float function to make sure that the computer recognizes
# the values in the table as numbers and not text
rowV = float(row[0]) * mach_conversion
# If v is equal to the current row velocity, we can return the Cd value
# directly from the table
if v - rowV == 0:
return row[1]
# If v is larger than the row velocity, we keep looking
elif v - rowV > 0:
bottom_index += 1
# If v is less than the current row, we know v is in between v1 and v2
elif v - rowV < 0:
# At this point, the bottom_index is at the current row (which is v2)
# so we set the top index as the row for v2 and Cdref2
top_index = bottom_index
# If we want the values for v1 and Cdref1,
# we need to get the row one before the current row.
v1 = float(G7Drag[bottom_index-1][0]) * mach_conversion
Cdref1 = float(G7Drag[bottom_index - 1][1])
# We then get the values for v2 and Cdref2
v2 = float(G7Drag[top_index][0]) * mach_conversion
Cdref2 = float(G7Drag[top_index][1])
# Using our linear interpolation formula
Cdref = (v - v1) / (v2 - v1) * (Cdref2 - Cdref1) + Cdref1
return Cdref
# Constants
pi = 3.14
g = 9.81
tdelta = 0.001
# Inputs
airDensity = 1.203
BC = 0.2
muzzleVelocity = 900
muzzleAngle = 0.1
windVelocity = 5
windAngle = 45
BC = 703.7 * BC
muzzleAngle = muzzleAngle * pi / 180
windAngle = windAngle * pi / 180
xinitial = 0
vxinitial = muzzleVelocity * cos(muzzleAngle)
yinitial = 0
vyinitial = 0
zinitial = 0
vzinitial = muzzleVelocity * sin(muzzleAngle)
vtotal = muzzleVelocity
wx = windVelocity * -1 * cos(windAngle)
wy = windVelocity * -1 * sin(windAngle)
xList = []
vxList = []
axList = []
yList = []
vyList = []
ayList = []
zList = []
vzList = []
azList = []
for i in range(0,1000):
# REST OF CODE
Now we need to tell the computer what we want to execute inside the for loop. We want it to calculate the acceleration, velocity, and positions like we did in the manual example:
Cdref = dragCoefficient(vtotal)
ax = -1/8 * Cdref / BC * pi * airDensity * (vxinitial-wx)**2
vxfinal = ax * tdelta + vxinitial
xfinal = vxinitial * tdelta + xinitial
ay = -1/8 * Cdref / BC * pi * airDensity * (vxinitial-wx) * (vyinitial-wy)
vyfinal = ay * tdelta + vyinitial
yfinal = vyinitial * tdelta + yinitial
az = -1/8 * Cdref / BC * pi * airDensity * (vxinitial-wx) * vzinitial - g
vzfinal = az * tdelta + vzinitial
zfinal = vzinitial * tdelta + zinitial
We have now calculated the accelerations, velocities, and positions of the projectile in the x,y, and z direction. Our next step is to add these to our list so that we won’t overwrite them when we run the calculation the next time. We do this by appending the output of the calculations to the python lists.
xList.append(xfinal)
vxList.append(vxfinal)
axList.append(ax)
yList.append(yfinal)
vyList.append(vyfinal)
ayList.append(ay)
zList.append(zfinal)
vzList.append(vzfinal)
azList.append(az)
The last thing we need to do inside this for loop is set the “initial” values to be the final values from this calculation. This will ensure the next calculation will start from where we left off.
vtotal = (vxfinal**2 + vyfinal**2 + vzfinal**2)**0.5
xinitial = xfinal
vxinitial = vxfinal
yinitial = yfinal
vyinitial = vyfinal
zinitial = zfinal
vzinitial = vzfinal
The for loop will run 1000 times and at the end we will have our list of data. If we print the data, this is what it looks like:
print("xList")
print(xList)
print("yList")
print(yList)
print("zList")
print(zList)
OUTPUT:
xList [0.8999986306114584, 1.7992788010089602, 2.6978413311478175, 3.5956870401640098, 4.4928167463735,...]
yList [0.0, -2.8102145981192093e-06, -8.427436587690136e-06, -1.6848461966819696e-05, -2.8070089941055e-05,...]
zList [0.0015699992037258414, 0.003128939998425155, 0.004676831606737141, 0.006213683238272165, 0.007739504089618864,...]
This data does not help us much, let’s graph it with the matplotlib library so we can have a visual look at the data.
To graph the y and z position vs the x position of the projectile:
trajectoryFig = plt.figure()
graph = trajectoryFig.add_subplot(411)
plt.ylabel("Z position")
plt.xlabel("X position")
plt.plot(xList, zList, 'b-')
plt.grid(True)
trajectoryFig.add_subplot(412, sharex=graph)
plt.ylabel("Y Position")
plt.xlabel("X position")
plt.plot(xList, yList, 'b-')
plt.grid(True)
plt.show()
The output should look like this:
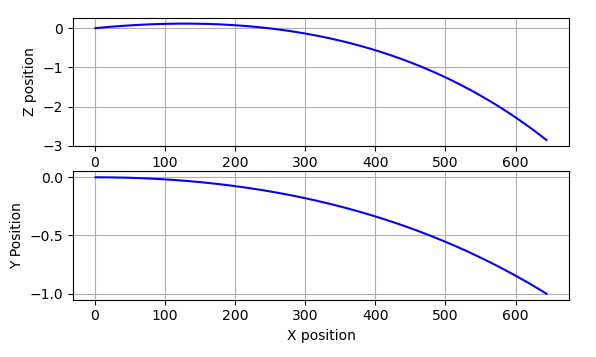
Conclusion
If you have made it this far, congratulations, that concludes our series on creating a ballistic calculator. This calculator is relatively primitive compared to some available online, but if you compare it to the others it still comes impressively close. If you are interested in taking this further, some easy features to add in would be compensating for different air density, targets that are elevated up or down, changing wind conditions down range, etc. If you are interested in the more advanced technical details, Modern Exterior Ballistics: The Launch and Flight Dynamics of Symmetric Projectiles by Robert L. McCoy is an incredible resource that formed the basis for much of this series.
If you would like to download the code, it can be found on my github here: Ballistic Calculator Source Code. Otherwise, here is the final code:
import matplotlib.pyplot as plt
from math import cos, sin
import csv
def dragCoefficient(v):
# We use 341.5 m/s as our conversion from m/s to mach speed
mach_conversion = 341.5
# Open up the csv file holding the table of reference Cd values
# IMPORTANT the file must be in the same location as this python script
# Change the "G7.csv " to the name of the csv file containing the data
with open("G7.csv") as G7DragFile:
# We create a list containing the rows from the table
G7Drag = list(csv.reader(G7DragFile))
# Interpolation (v - v1) / (v2 - v1) = (Cdref - Cdref1) / (Cdref2 - Cdref1)
# Cdref = (v - v1) / (v2 - v1) * (Cdref2 - Cdref1) + Cdref1
# The bottom index will keep track of the last row the computer looked at
bottom_index = 0
# The computer will need to check the velocity for each row of the table,
# until we find the two rows (v1 and v2) that are greater and less than v
for row in G7Drag:
# We use the float function to make sure that the computer recognizes
# the values in the table as numbers and not text
rowV = float(row[0]) * mach_conversion
# If v is equal to the current row velocity, we can return the Cd value
# directly from the table
if v - rowV == 0:
return row[1]
# If v is larger than the row velocity, we keep looking
elif v - rowV > 0:
bottom_index += 1
# If v is less than the current row, we know v is in between v1 and v2
elif v - rowV < 0:
# At this point, the bottom_index is at the current row (which is v2)
# so we set the top index as the row for v2 and Cdref2
top_index = bottom_index
# If we want the values for v1 and Cdref1,
# we need to get the row one before the current row.
v1 = float(G7Drag[bottom_index-1][0]) * mach_conversion
Cdref1 = float(G7Drag[bottom_index - 1][1])
# We then get the values for v2 and Cdref2
v2 = float(G7Drag[top_index][0]) * mach_conversion
Cdref2 = float(G7Drag[top_index][1])
# Using our linear interpolation formula
Cdref = (v - v1) / (v2 - v1) * (Cdref2 - Cdref1) + Cdref1
return Cdref
# Constants
pi = 3.14
g = 9.81
tdelta = 0.001
# Inputs
airDensity = 1.203
BC = 0.2
muzzleVelocity = 900
muzzleAngle = 0.1
windVelocity = 5
windAngle = 45
BC = 703.7 * BC
muzzleAngle = muzzleAngle * pi / 180
windAngle = windAngle * pi / 180
xinitial = 0
vxinitial = muzzleVelocity * cos(muzzleAngle)
yinitial = 0
vyinitial = 0
zinitial = 0
vzinitial = muzzleVelocity * sin(muzzleAngle)
vtotal = muzzleVelocity
wx = windVelocity * -1 * cos(windAngle)
wy = windVelocity * -1 * sin(windAngle)
xList = []
vxList = []
axList = []
yList = []
vyList = []
ayList = []
zList = []
vzList = []
azList = []
for i in range(0,1000):
Cdref = dragCoefficient(vtotal)
ax = -1/8 * Cdref / BC * pi * airDensity * (vxinitial-wx)**2
vxfinal = ax * tdelta + vxinitial
xfinal = vxinitial * tdelta + xinitial
ay = -1/8 * Cdref / BC * pi * airDensity * (vxinitial-wx) * (vyinitial-wy)
vyfinal = ay * tdelta + vyinitial
yfinal = vyinitial * tdelta + yinitial
az = -1/8 * Cdref / BC * pi * airDensity * (vxinitial-wx) * vzinitial - g
vzfinal = az * tdelta + vzinitial
zfinal = vzinitial * tdelta + zinitial
xList.append(xfinal)
vxList.append(vxfinal)
axList.append(ax)
yList.append(yfinal)
vyList.append(vyfinal)
ayList.append(ay)
zList.append(zfinal)
vzList.append(vzfinal)
azList.append(az)
vtotal = (vxfinal**2 + vyfinal**2 + vzfinal**2)**0.5
xinitial = xfinal
vxinitial = vxfinal
yinitial = yfinal
vyinitial = vyfinal
zinitial = zfinal
vzinitial = vzfinal
trajectoryFig = plt.figure()
graph = trajectoryFig.add_subplot(411)
plt.ylabel("Z position")
plt.xlabel("X position")
plt.plot(xList, zList, 'b-')
plt.grid(True)
trajectoryFig.add_subplot(412, sharex=graph)
plt.ylabel("Y Position")
plt.xlabel("X position")
plt.plot(xList, yList, 'b-')
plt.grid(True)
plt.show()