Recap

In the previous section we discussed core math concepts required to understand projectile motion.

• The Cartesian coordinate system will allow us to mathematically describe the position, velocity, and acceleration of an object.

• Vectors allow us to describe the the direction and magnitude of velocity and acceleration

• Algebra and trigonometry will help us solve the equations of motion of the projectile

Kinematic Equations

The kinematic equations relate the effects of position, velocity, and acceleration to each other. These equations are commonly applied in examples where an object is accelerated by gravity.

The kinematic equations have the following form (using the z direction as an example):

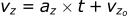
• vz : velocity in z direction(m/s)
• az : acceleration in z direction (m/s²)
• t : time (s)
• vzo: starting velocity in z direction (m/s)

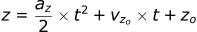
• z: position of the ball in z direction(m)
• az : acceleration in z direction (m/s²)
• t : time (s)
• vzo: starting velocity in z direction (m/s)
• zo : starting position in z direction (m)

Understanding simplified 1D projectile trajectory

The best way to start to understand projectile trajectory is with a basic, ideal scenario.

A common case study when introducing physics in school is the idea of throwing a ball in the air and allowing it to fall back to the ground. We want to know how long it takes to return to the ground when thrown.

Let’s define the scenario.

• The ball is thrown vertically upward at a velocity of 10 m/s
• The ball is thrown from 1 m above the ground
• There is no air resistance

Another way to frame the question, we want to determine the acceleration, velocity, and position of the ball at all points in its trajectory. We can start by using the equations we defined before.

If there is no air resistance, gravity is the only force acting to accelerate the ball. The acceleration of gravity is -9.8 m/s². Since we define our coordinate system with the positive direction going up, the negative sign indicates that the gravity is acting in the downward direction. This is what pulls the ball back to the ground when thrown.

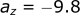
Going back to the question, we are interested in knowing how long the ball will take to return to the ground. This will require manipulating the kinematic equations, but first let’s make a list of the information we know:

• z = 0 m
• zo = 1 m
• vzo = 10 m/s
• az = -9.8 m/s²

If we input these values into the equation for the z position:

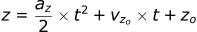
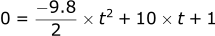
You may recall from algebra that this is a quadratic equation.

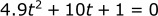
These can be solved using the quadratic formula:

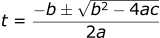
Where:

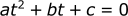
Plugging the numbers in, we get two solutions:

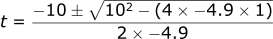
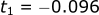
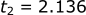
Since negative time does not make sense in this problem, we know the solution is that it takes 2.14 s for the ball to return to the ground.

Next article: Calculating 2D Trajectory