Recap

We have seen a basic 1D trajectory problem. With 1D projectile motion, we were only concerned with the vertical movement of a ball. This movement was defined by the kinematic equations:

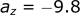
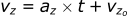
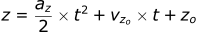
We solved the position equation to get the time (t) when the ball returns to the ground (z=0). With 1D projectile motion, the examples are restricted to throwing the object perfectly vertical. In most cases the object is thrown at some angle. To solve this new problem, we need two dimensions [x,z] to describe this motion.

Understanding simplified 2D projectile trajectory

As seen in the previous example, 1D projectile trajectory is fairly simplistic in nature. 2D projectile motion requires slightly more advanced math, but provided air resistance is neglected, it can still be easily calculated.

With 2D projectile motion, the path of the ball is no longer vertically up and down. The path of the ball will follow a parabola and have both a vertical and horizontal position.

As such, we need to define the equations in the x (horizontal) and z (vertical) direction.

The equations describing vertical motion remain the same:

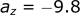
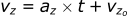
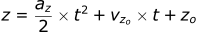
The equations describing horizontal motion are similar, but since there is no air resistance (or gravity in the horizontal direction), there is no acceleration in this direction.

Acceleration:

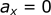
Velocity:

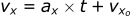
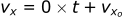
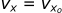
Position:

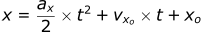
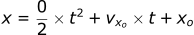
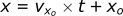
To solve for the overall position of the projectile, both equations need to be solved for the x and y position.

To summarize with an example:

Example 1

A ball is thrown upward at a 45 degree angle. Find:

1. How long it takes to reach the ground
2. The [x,z] position of the ball at its highest position
3. The horizontal position when the ball reaches the ground.

The initial conditions are:

• The ball is thrown with a velocity of 10 m/s
• The ball is thrown from 1 m above the ground
• There is no air resistance

For the x-direction:

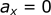
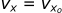
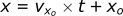
• x = ?
• xo = 0 m
• vxo = 10 m/s * cos(45deg) = 7.07
• ax = 0 m/s²
• t = ?

For the z-direction:

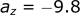
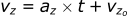
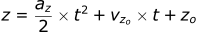
• z = 0 m
• zo = 1 m
• vzo = 10 m/s * sin(45deg) = 7.07
• az = -9.8 m/s²
• t = ?

Part 1.

To solve this problem, the critical piece of understanding is that only the vertical (vz) component of the velocity determines the time the ball remains in the air. The ball will continue to move in the horizontal (x) direction for as long as the ball remains in the air (until z=0) because there is nothing decelerating it.

Solving for the time (t) the ball remains in the air (by setting z=0):

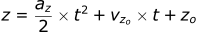
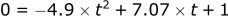
Using the quadratic solver the same as in part 1:

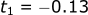
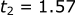
Rejecting the negative solution, the ball is in the air for 1.57s.

Part 2.

To determine the [x,z] position of the ball at its highest position, the trick is that the velocity of the ball will be zero when it reaches its highest point. This makes intuitive sense, when the ball is thrown in the air it starts slowing down (because of gravitational acceleration) until it reaches the highest point (vz = 0). The ball's velocity then increases as it falls back toward the ground.

To determine the [x,z] location of the ball at the highest point, the time when the ball has zero vertical velocity (vz = 0) needs to be solved for.

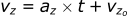
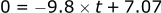
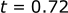
If we solve for the x and z position at this time (t = 0.72 s):

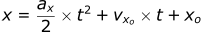
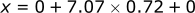
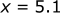
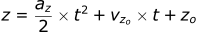
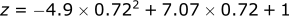
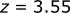
The [x,z] position of the ball at the highest point in its arc is [5.1, 3.55] meters.

Part 3.

To determine the horizontal position when the ball hits the ground, we use the time from Part (a) (when z=0) in the equation defining the x position.

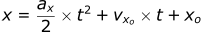
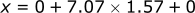
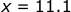
The ball hits the ground 11.1 meters from where it was thrown.

Graphing the trajectory

If we want, we can also graph the trajectory of the projectile. Both x and z are functions of time, however, for most trajectory problems we want to know the height of a projectile as a function of its distance. Since both functions are only a function of time, we can combine them together with some algebra.

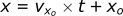
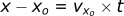
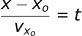
If we substitute this equation into the z position equation replacing t:

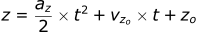
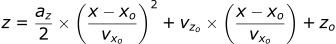
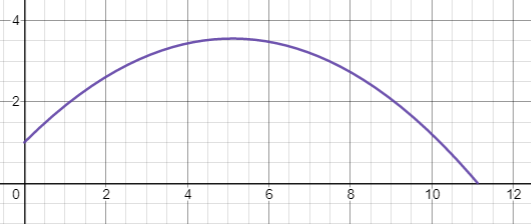
If we plot this final equation:

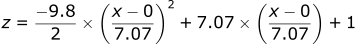
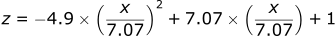
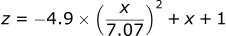
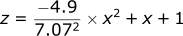
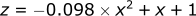
Plot of z = -0.098x² + x + 1

We can confirm our solutions above:

• The highest point the ball reaches is 3.55 m
• The ball reaches 11 m in the x direction before hitting the ground

Although this example is simplistic in nature, it builds the foundation for how we approach the more difficult problems.

To see how this might apply to a bullet being fired from a rifle, let’s see an example:

Example 2

A rifle shoots a bullet with a velocity of 2700 feet per second. The rifle is held perfectly horizontal when fired (from a distance 1 m above the ground). How far does the bullet travel before it hits the ground? Assume there is no air resistance.

We will continue using the equations from the above example:

For the x-direction:

Acceleration ax:

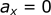
Velocity vx:

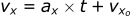
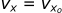
Position x:

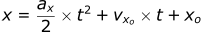
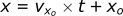
For the z-direction:

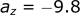
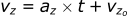
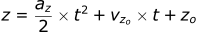
The information we know:

• ax = 0

• vxo = 2700 fps

• xo = 0

• az = -9.8 m/s²

• vzo = 0

• zo = 1 m

• z = 0

What we need to solve for:

• x = ?
• t = ?

Following the same process above, we solve for t first:

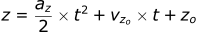
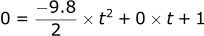
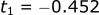
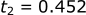
The bullet is in the air for 0.452 s before it hits the ground.

Using this knowledge, we solve for the x position at t = 0.452 s.

First we convert ft/s into m/s:

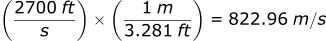
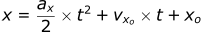
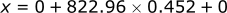
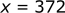
If we want we can convert back into feet:

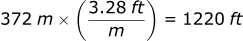
We now know that the bullet would travel 372 m (1220 ft) before it hits the ground.

Let’s plot this trajectory as well using the equation we derived before:

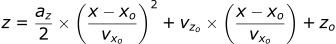
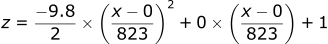
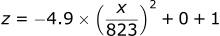
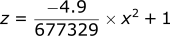
Plotting the graph:

Plot of z = -(4.9/677329)x² + 1

The projectile hits the x axis at 372, the same as we calculated above.

Next article: Calculating Trajectory: Aerodynamic Drag and Ballistic Coefficient