Recap

In the previous article we covered how to calculate the motion of a 2D trajectory. An objects motion is typically not restricted to 1 dimension, using 2 dimensions, we were able to analyze more general scenerios.

To simplify the previous examples, we have been neglecting air resistance. This is largely unrealistic as the aerodynamic drag forces have a large impact on the trajectory of an object, especially fast-moving objects. We will now go through how we account for this in our calculations.

Aerodynamic drag

Understanding the fundamentals of aerodynamic resistance is a very complex topic. Luckily, despite its complicated nature, it is simple to implement in our calculations.

This is the equation for aerodynamic drag which we can use to improve the accuracy of our model:

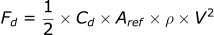
• Fd: Drag force (N)
• Cd: Drag coefficient (no dimensions)
• Aref: Reference area (commonly cross-sectional area) (m²)
• ρ: Density of fluid (kg / m³)
• v: Velocity of projectile (m/s)

From looking at the equation we can determine the following facts about the drag force:

• The greater the fluid density, the more drag on the projectile
• As the projectile moves faster, the drag force will increase proportional to v². If the projectile moves twice as fast, the drag will be 4 times larger.
• As the projectile increases in size, the drag increases proportionally.

Aerodynamic resistance is a combination of many different forces acting on the projectile to slow it down. For example, you have drag from the fluid "rubbing" the side of the projectile as it moves through it. You also have drag from the projectile trying to move the fluid in front of it out of the way. In order to account for these complex forces, the drag coefficient is used to combine the effects of all of these forces to simplify the overall equation. This coefficient in general cannot be calculated and is found experimentally.

Note: This equation applies for fluids, as such, it can also be applied to an object moving through a liquid such as water. However, for our applications we will only be considering the drag of a projectile in air.

Recalling the equations from the previous sections:

For the x-direction:

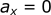
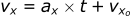
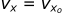
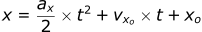
For the z-direction:

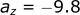
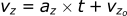
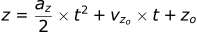
Acceleration in the x-direction (ax) was set to 0 because we neglected aerodynamic resistance. If we want to account for this drag, we can no longer do that. However, you may have noticed the equation we have for aerodynamic resistance uses force and not acceleration. We need to address this before we can move any farther.

Newton's Second Law:

Newton’s second law relates the force on an object to its acceleration and mass. The heavier an object is, the harder you need to push to accelerate it. The harder you push an object, the larger the acceleration.

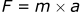
• F: Force on object(N)
• m: Mass of object (kg)
• a: Acceleration of object (m/s²)

We can use this law to turn our drag force into the drag acceleration on the projectile by combining the equations:

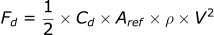
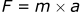
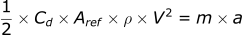
Since we want acceleration, we rearrange the equation:

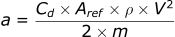
This is the acceleration on the bullet caused by the aerodynamic drag force.

Side Note - Ballistic Coefficient

As it pertains to bullets, you may see a "Ballistic Coefficient" (BC) listed for a particular bullet. It is important to note that this is different from the drag coefficient Cd. In this section we will explain how the Ballistic Coefficient makes our calculations more convenient.

IMPORTANT: The BC unit is normally listed without units by the manufacturer, however, conventionally it is in lb/in². For the sake of our calculator, we are keeping everything in SI units. We will need to convert the manufacturer BC values to kg/m² units. The conversion is 703.7 kg/m² = 1 lb/in².

The Ballistic Coefficient (BC) considers the mass and size of the projectile in addition to the drag coefficient. It is defined as follows:

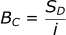
• SD: Sectional Density of bullet (kg/m²)
• i: Ratio of actual drag coefficient vs reference drag coefficient (explained later)

The formulas for SD and i are:

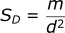
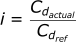
If we combine these equations we get:

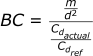
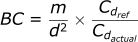
• BC: Ballistic Coefficient (kg/m²)
• m: Mass (kg)
• d: Diameter of projectile (m)
• Cdbullet: Drag coefficient of projectile (No units)
• Cdref: Drag coefficient of a reference projectile (No units)

Most of these terms we have seen before, but let’s quickly break down what the Cdref is.

Reference Cd values

You may have been wondering why we bother creating a new term BC instead of the manufacturer providing the actual drag coefficient (Cd) directly. Speaking to the complexities of aerodynamic resistance, the value of the drag coefficient changes depending on different conditions (speed, flow direction, etc.). This is especially important with the fast moving projectiles such as bullets that can go faster than the speed of sound. Since your Cd value will change as the bullet decreases in speed, how would you know which value for Cd to pick?

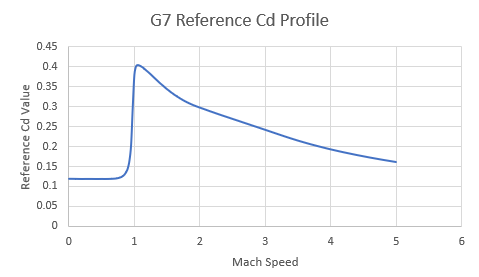
To solve this problem, the drag coefficient of generic bullet shapes were measured across a range of mach numbers (Cdref). The mach number is the ratio of the velocity of an object against the speed of sound in a fluid (see below). There are a number of different reference profiles, typically listed as G1, G2, ... , G7, etc. Since we are developing a ballistic calculator for a rifle, G1 and G7 profiles are the most appropriate.

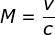
• M: mach number
• v: velocity (m/s)
• c: speed of sound (m/s)

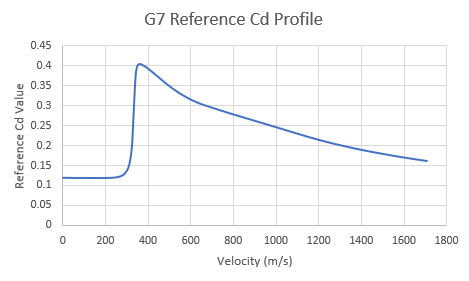
NOTE: It is important we draw attention to the fact that the drag coefficient is measured against the mach number. The speed of sound in a fluid is affected by temperature which subsequently will change the mach number. For our calculations we will assume International Civil Aviation Organization (ICAO) atmospheric conditions (15 deg C), which results in a speed of sound of 340.3 m/s in air. Similarly, we will use the ICAO standard conditions for the air density (1.225 kg/m⊃3).

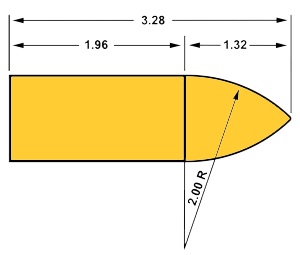
Back to the profiles of the bullets, the G1 profile is based around a flat-based bullet. The G7 profile is for boat-tail bullets (most rifle bullets) and is generally more appropriate for precision or long-distance shooting. Manufacturers will generally list which reference profile they use for the particular bullet.

G7 Profile Shape

G1 Profile Shape

Here are the plots of the G7 drag profiles:

G7 Profile: Cdref vs Mach speed

G7 Profile: Cdref vs Velocity (m/s) @ ICAO Conditions: 15 deg C, Mach = 340.3 m/s

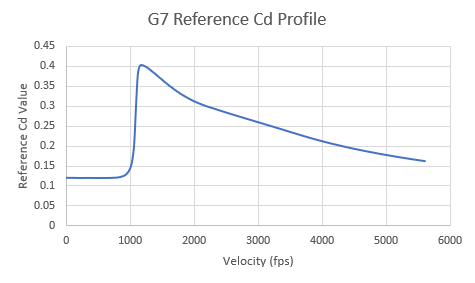
G7 Profile: Cdref vs Velocity (ft/s) @ ICAO Conditions: 59 deg F, Mach = 1116.5 fps

If the manufacturer measures the actual Cd of their bullet across the same range of velocities as the reference profiles, when you compare the two graphs the actual Cd of the bullet should appear like a scaled version of the reference profile.

By taking the ratio of the actual drag profile against the reference profile, the manufacturer can report a single number instead of a table of values while still maintaining reasonable accuracy. This makes it simple for the end user to enter information into a ballistic calculator, you can enter one number instead of a table of 100's of values.

Now if we are the ones creating the ballistic calculator, we can use some algebra to take the manufacturer's BC value and convert our equation of acceleration to include the reference Cd value for which we already have a table of values. Let's work through this process.

We first need to rearrange the BC equation so that we get the actual Cd value:

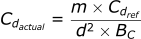
Now we can substitute this equation into the drag equation from earlier:

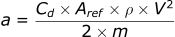
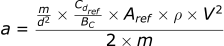
If we recognize that the formula for area is:

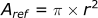
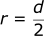
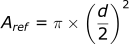
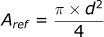
The formula then becomes:

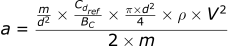
You will notice that the mass (m) and diameter (d²) cancel out:

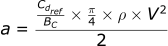
Our final equation simplifies to this:

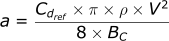
Now you can see why the definition of BC also includes the mass (m) and diameter (d²) terms; it greatly simplifies the overall equation.

Next article: Calculating Trajectory: Modelling 3D Bullet Trajectory