Recap

In the last section, we covered the equation defining air resistance. Then we modified the drag force equation into an acceleration equation which we are more familiar with.

Our final equation for the drag acceleration was:

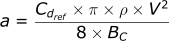
We now have all the tools we need to put together a model for a realistic scenario.

Modelling 3D bullet trajectory

To this point, we have made a number of assumptions to calculate the simplified trajectory for the 1D and 2D cases.

In order to calculate the trajectory of a projectile like a bullet, we need to develop and understand the comprehensive list of what assumptions we can and cannot make to have an accurate calculation.

Common approximations for projectile trajectory

• Air resistance must be considered in our calculations.
• The wind acting on the bullet has a velocity much slower than the bullet velocity (w << v)
• The bullet will be treated as a point mass. By making this assumption, we neglect any effect that the shape of the bullet would have on the trajectory during flight.

IMPORTANT: This assumption neglects the effects of bullet spin, pitch, and yaw on the trajectory. This is an idealized case and serves to make calculation easier without diminishing the accuracy of the end result significantly. If you were to shoot very long distances, we would need to consider these effects. However, this increases the complexity of our model significantly and is beyond the scope of these articles.

Non-ideal case (exaggerated for illustration)

Ideal case

Although we approximate the bullet as a point mass, we will still consider the shape of the bullet when calculating the aerodynamic drag (the Cdref value is a related to the shape of the G1 or G7 profile).

Calculating the trajectory

The first thing to consider is that the realistic trajectory of a bullet is not restricted to 2D motion. We will need to update our model to account for 3D motion. Since we have taken small steps to get to this point, this should be easy to follow. We will also need to implement implementing air resistance and wind into the equations.

Our coordinate system will be set up as follows:

• x axis extends from the shooter to the down range target
• y axis extends perpendicular to the X-axis horizontally along the ground (right to left of shooter)
• z axis extends in the same direction as gravity (vertical direction)

We will start by listing the equations of motion and work our way backwards to see how they were derived.

x-direction

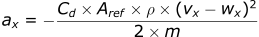
• ax : acceleration in x direction (m/s²)
• Cd : drag coefficient
• Aref : Projectile reference area (m²)
• ρ : Air density (kg/m³)
• vx : velocity of projectile in x direction (m/s)
• wx : wind velocity in x direction (m/s)
• m : mass of projectile (kg)

y-direction

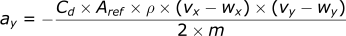
• ay : acceleration in y direction (m/s²)
• vy : velocity of projectile in y direction (m/s)
• wy : wind velocity in y direction (m/s)

z-direction

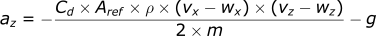
• az : acceleration in z direction (m/s²)
• vz : velocity of projectile in z direction (m/s)
• wz : wind velocity in z direction (m/s)

If we look back to the original equation for projectile drag, these equations should look similar with the only differences being the introduction of wind terms (wx, wy, wz).

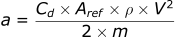
From looking at these equations, one question you may have is why is there a (vx-wx) term in the equations for the y and z directions? Without going too deep into the math (if you are interested, this is explained in detail in Modern Exterior Ballistics by Robert McCoy), we can try and intuitively explain what is going on.

Looking back to the original drag equation:

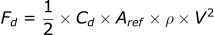
This equation does not account for any directionality, and assumes the absolute speed of the projectile. Since we have split our equations of motion into three different directions (x,y,z), this equation needs to be modified accordingly.

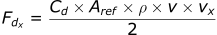
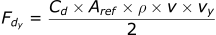
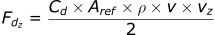
• Fdx : Drag force in x direction (N)
• Fdy : Drag force in y direction (N)
• Fdz : Drag force in z direction (N)
• v : Absolute velocity of projectile (m/s)
• vx : Velocity of projectile in x direction (m/s)
• vy : Velocity of projectile in y direction (m/s)
• vz : Velocity of projectile in z direction (m/s)

To calculate the absolute velocity of the projectile, this formula is used:

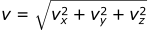
The bullet fired from a rifle will have a much larger velocity in the x direction than in the y or z direction. With this assumption, we can claim that the absolute velocity is approximately the same as vx.

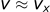
Substituting this into the Drag equations, we get:

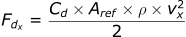
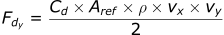
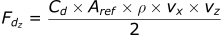
The last step is to incorporate the wind term. To reintroduce the wind terms, replace vx with (vx-wx), vy with (vy-wy), and vz with (vz-wz).

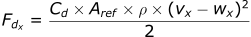
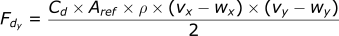
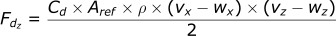
Re-using Newton’s Second Law, for x-direction:

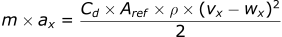
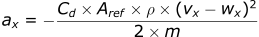
For y-direction:

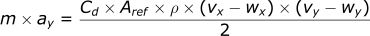
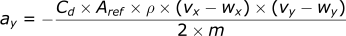
For z-direction:

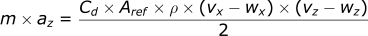
We need to add the acceleration of gravity into the equation as well

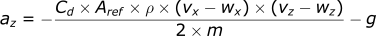
We have finally come full circle and arrived at the equations from the beginning of the section.

Clarifying the wind term in the equation

In the equation, the wind is always subtracted from the velocity of the projectile. Why does the equation show it always slowing down the projectile? What happens when the wind is blowing downrange (a tailwind)? Wouldn't this speed up the projectile slightly? This slight confusion can be clarified easily if we evaluate a few cases with trigonometry.

Typically, you would characterize the wind as blowing from a certain direction on the compass rose.

For example, what about if you are facing North and a 2 m/s wind is blowing from the South-West. To use this in our calculations, we need to break down the wind into its x and y directions. This is done using the cosine and sine functions respectively.

For wind in the x-direction:

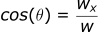
We added a negative to this equation to flip the answer. This is because our convention is based on the direction the wind is blowing from not the direction the wind is blowing to. This will make more sense when we evaluate an example.

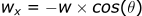
Wind in the y-direction:

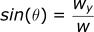
This equation also has the negative to flip the answer.

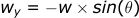
Standard convention has an angle of 0 degrees along the x axis, and the angle increases in a counter-clockwise rotation.

In our example, the x direction is pointed North. Therefore, the angle of the South-West direction would be:

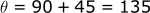
Using the above equations:

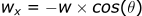
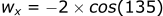
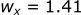
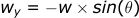
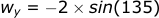
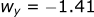
Let's see how the wind affects the projectile velocity:

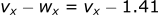
In the x-direction the wind decreases the effective velocity, which will decrease the drag (drag proportional to v²). This intuitively makes sense because it is a tailwind.

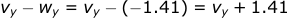
For the y-direction, the bullet starts with zero velocity. This means the wind will start pushing the bullet in the East direction (-y direction) immediately after firing. Once the bullet starts moving in this direction, the wind acts like a tailwind, so the drag will decrease over time.

Reintroducing the Ballistic Coefficient

At this point, let’s introduce the ballistic coefficient into these equations to reach the simplified version:

For the x-direction:

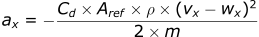
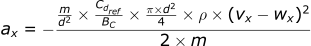
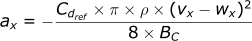
For the y-direction:

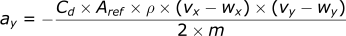
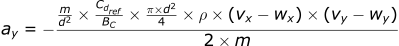
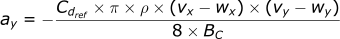
For the z-direction:

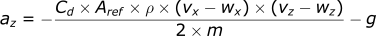
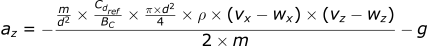
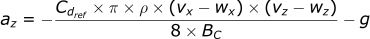
The last assumption we can make is to ignore any wind in the vertical (z) direction. Typically, the wind is much stronger in the x and y directions compared to the z direction. If we remove the wz term, it does not make a meaningful difference to the accuracy of the calculations.

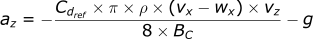
We now have the equations of motion describing the system, we will demonstrate how to evaluate these equations in the next section.

Next article: Calculating Trajectory: Analytical vs Numerical Methods