Recap

To this point, we have a list of the equations that define the motion of a projectile in 3D space. There are some key differences from our latest model compared to the 1D and 2D trajectory cases. We are now accounting for:

• Aerodynamic drag acting on the object
• Wind acting on the object

Our final list of equations:

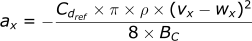
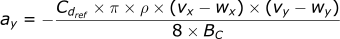
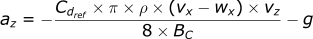
In this section, we will cover how we can solve these equations.

Analytical vs Numerical methods

An analytical solution is defined as an exact solution for a problem. A numerical solution is an approximation of the solution which is found with a numerical method.

Analytical solutions can be hard to use for more complex problems, and in some cases, one may not exist.

If you recall back to the articles on 1D and 2D trajectories, we used analytical solutions. In the equation describing the position (z), as long as you know the initial velocity (vzo) and the initial position (zo), if you plug in any time (t) you get the position of the object.

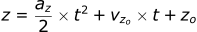
An analytical solution gives the exact solution, but unfortunately, as the mathematical problems get more complicated, they are incredibly difficult if not impossible to derive.

On the other hand, numerical methods give an approximation to the solution. Numerical solutions are typically computationally limited, however, they can be used with success on very difficult problems.

We can use an example to showcase the differences in a practical sense.

Let's say we have a polynomial in the form of:

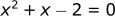
To solve this analytically, we can use our quadratic formula:

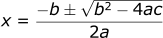
Where:

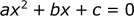
Plugging in the values from the polynomial:

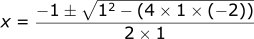
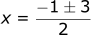
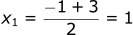
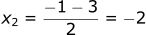
To solve this numerically, what if we just tried a bunch of different numbers and checked if it works? This is the most primitive example of numerical methods but it gets the point across. A computer is great at doing things really fast, for it to guess and check thousands of numbers would take less than a second.

Lets start with x = 0:

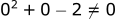
Lets try x=1:

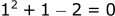
We found one solution.

Lets try x=2:

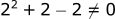
We are getting further away from 0, let's try going the other direction.

Trying x=-1:

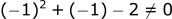
Trying x=-2:

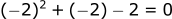
We found the second solution.

This method can be applied to very complex problems where an analytical solution is not possible. Coincidentally, to solve our new set of equations which incorporates wind-resistance, we will need to use numerical methods as an analytical solution cannot be derived.

There are many different computational methods to approximate a solution to these types of problems, we will show a practical example by solving a problem incorporating wind resistance and then explain how it works after.

The basis of our computational method will be to calculate the equations of motion over and over again, each time taking an incremental step in time.

If we go back to the section where we reviewed acceleration, velocity, and position, you may recall the two conditions to use those equations:

• The position or velocity change has to be constant over the period of time
• OR the time interval is very small (which allows for case 1 to be assumed)

We know that both the velocity and the position do not change at a constant rate over the duration of the projectile’s flight. However, with computational methods, we can make use of the second condition.

If we use a very small time interval (small tdelta), we can make the assumption that the acceleration over that time interval will not change. If we know that the acceleration is not changing, we can calculate the velocity at the end of the step by re-arranging this equation:

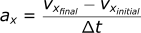
If we want the final velocity (vxfinal) we can rearrange this equation:

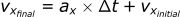
Computers are great at doing repetitive tasks, these computational methods make use of this by computing these equations many, many times over very small intervals.

The position can also be found in a similar way by rearranging the velocity equation:

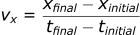
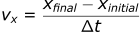
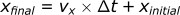
To make this more understandable, let’s review an example:

A bullet (BC of 0.2 lb/in² using G7 drag profile) is shot out of a rifle and leaves the muzzle with a speed of 900 m/s (~2950 fps). The rifle is fired perfectly horizontal from a height of 1 m above the ground. There is no wind. Air density is 1.203 kg/m³

Key information:

• BC = 0.2 lb/in² (G7 profile) = 140.74 kg/m²
• Air density = 1.203 kg/m³
• vinitial = 900 m/s
• vxinitial = vinitial (bullet is fired perfectly horizontal)
• zinitial = 1 m

Let’s start at t=0 and define that as the point when the bullet leaves the barrel at maximum velocity. We will use a small tdelta of 0.01 s.

Note: Using a smaller tdelta will typically increase the accuracy of the calculator, however, this is at the expense of taking longer for the computer to calculate the solution.

Since there is no wind we only need to worry about the x and z direction of the projectile.

Here are our equations for the acceleration of the projectile:

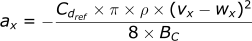
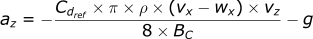
We can neglect any wind so they simplify:

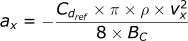
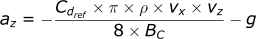
Starting from t=0:

• xinitial = 0 m
• vxinitial = 900 m/s
• zinitial = 1 m
• vzinitial = 0 m/s
• Cdref (G7 profile @ 900m/s) = 0.262 (We will describe how to get this later)
• BC = 140.74 kg/m²
• ρ = 1.203 kg/m³

Calculating the acceleration in the x-direction:

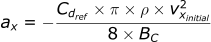
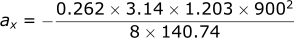
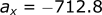
Calculating the velocity in the x-direction:

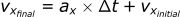
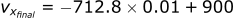
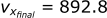
Calculating the position in the x-direction:

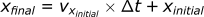
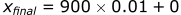
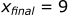
Calculating the acceleration in the z-direction:

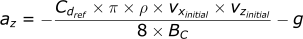
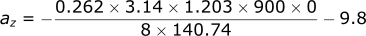
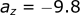
Calculating the velocity in the z-direction:

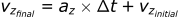
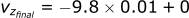
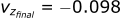
Calculating the position in the z-direction:

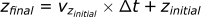
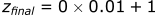
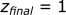
After 0.01 seconds, the bullet's new x velocity is 893 m/s and it now has a velocity in the z direction of -0.1 m/s. Now, we can start the process all over again, using these new velocities as the "initial" velocities for the next step at t=0.01.

Step 2, t=0.01:

The only values that have changed are the velocities and the Cdref.

• xinitial = 9 m
• vxinitial = 893 m/s
• zinitial = 1 m
• vzinitial = -0.1 m/s
• Cdref (G7 profile @ 893m/s) = 0.263

Calculating the acceleration in the x-direction:

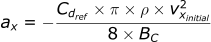
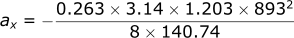
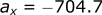
Calculating the velocity in the x-direction:

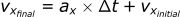
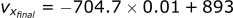
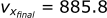
Calculating the position in the x-direction:

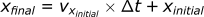
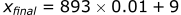
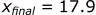
Calculating the acceleration in the z-direction:

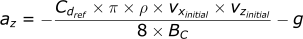
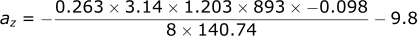
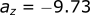
Calculating the velocity in the z-direction:

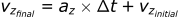
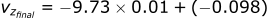
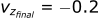
Calculating the position in the z-direction:

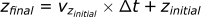
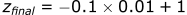
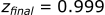
Step 3, t=0.02:

• xinitial = 17.93 m
• vxinitial = 885 m/s
• zinitial = 0.999 m
• vzinitial = -0.2 m/s
• Cdref (G7 profile @ 885m/s) = 0.265

Calculating the acceleration in the x-direction:

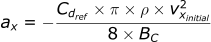
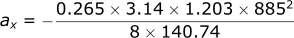
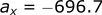
Calculating the velocity in the x-direction:

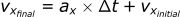
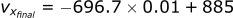
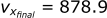
Calculating the position in the x-direction:

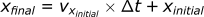
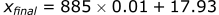
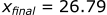
Calculating the acceleration in the z-direction:

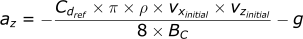
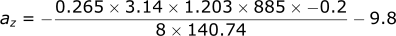
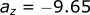
Calculating the velocity in the z-direction:

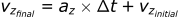
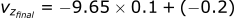
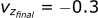
Calculating the position in the z-direction:

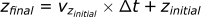
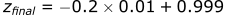
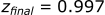
To summarize the first three steps of the calculation, after 0.03s into the bullets flight it has:

• Moved 26.79 m in the x-direction
• Moved -0.003 m in the z-direction (dropped 0.003 m from shooting position)
• A velocity in the x-direction of 878.9 m/s
• A velocity in the z-direction of -0.3 m/s

You can imagine manually calculating each of these steps would be extremely time consuming, to have a full picture of the bullet's trajectory would require repeating this hundreds of times. Luckily, if we program the computer to perform these calculations for us, those calculations can happen in fractions of a second.

Next article: Calculating Trajectory: Linear Interpolation of Reference Drag Coefficient