Overview

This article will review the fundamental math concepts required to understand the physics of projectile motion. Most of the information contained in this section is elementary and highschool level math, feel free to skip lessons if you are already comfortable with the concepts.

Key Points

• Coordinate systems
• Basic algebra
• Basic trigonometry
• Vectors
• Acceleration, velocity, and position

Coordinate Systems

In order to understand the math that is to follow, we must have a solid understanding of what a coordinate system is. We will be using the Cartesian coordinate system.

You may recall from grade school math, a graph typically has an x and y axis perpendicular to each other. The x-axis is located at the bottom of the graph (horizontal), the y-axis is along the side (vertical). With these two axes, you can describe a point on the graph.

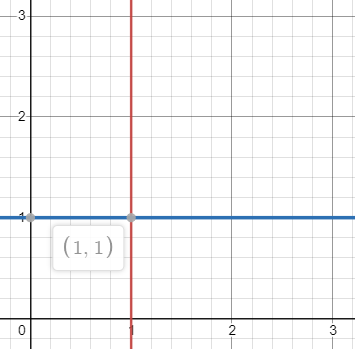Example: Point at x = 1, y = 1

The Cartesian coordinate system uses an x, y and z axis (all perpendicular to each other) to define a position with math. See below.

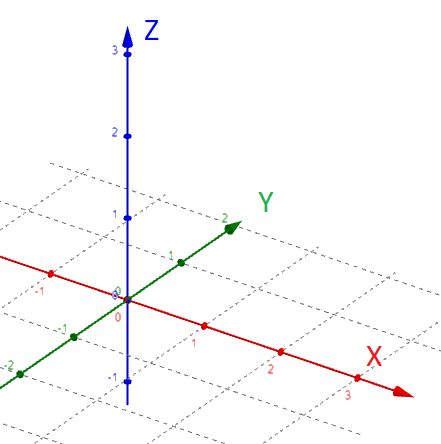Cartesian Coordinate System

In our context, these x, y, and z numbers will be referring to the position of a projectile in space. In an upcoming section we will see an example where we discuss acceleration, velocity, and position using Cartesian coordinates.

Basic Algebra

Throughout this series of articles we will be using basic algebra to re-arrange and solve equations. Basic trajectory physics problems encounter polynomials frequently, as such, we need to know how to solve them.

The polynomials we will be dealing with are 1st and 2nd degree. A first degree polynomial has the following form:

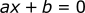
A second degree polynomial:

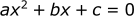
Where a, b, and c are numeric coefficients.

In our trajectory examples, the variable x will be replaced with t (time):

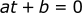
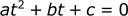
As an example, a first and second degree polynomial could look like this:

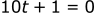
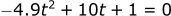
A first degree polynomial is easy to solve with basic algebra:

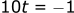
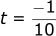
A second degree polynomial is harder and can have up to two solutions where the function is at 0.

If we look at a graph of the polynomial, we can see that at roughly t=-0.1 and t=2.1 the function is 0.

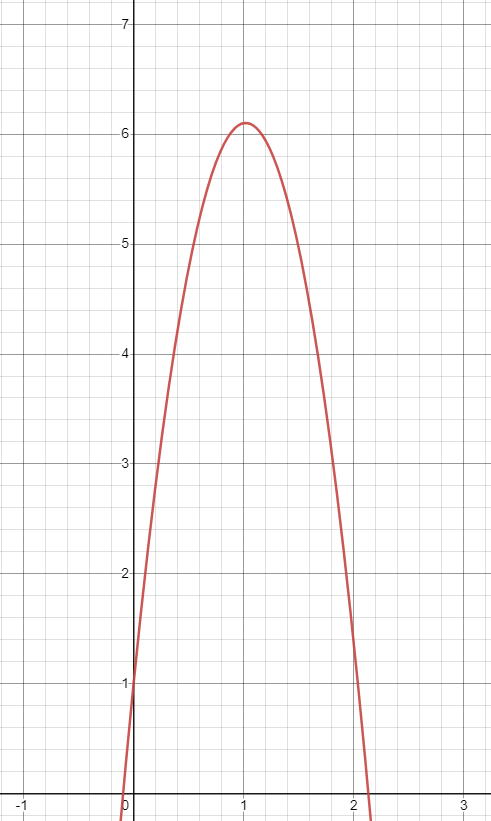Graph of z = -4.9t² + 10t + 1

There is also a formula which will give us the exact answer, the quadratic formula.

The formula takes the following form:

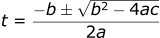
Where:

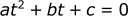
If we plug our numbers into the formula:

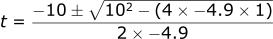
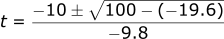
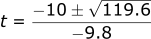
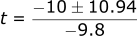
Solving for t1:

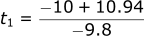
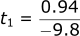
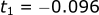
Solving for t2:

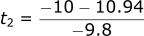
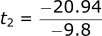
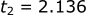
As you can see, our approximations from looking at the graph were reasonably close. However, quadratic formula gives the EXACT answer we are looking for. We will use this formula when we talk about 1D and 2D trajectory in the following articles.

Basic trigonometry

Basic knowledge of trigonometry will be required in order to calculate all but the most simple trajectory situations. We will cover a quick refresher of the important concepts:

Right angle triangles:

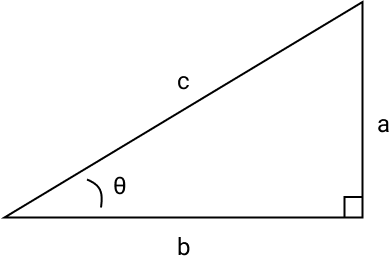
The trigonometry we are concerned with is how to use Pythagoras' theorem, and the sine, cosine, and tangent functions.

Pythagoras' Theorem

If you recall, with Pythagoras' theorem you can determine the length of any side of a right angle triangle as long as you have the other 2. The formula for Pythagoras' theorem is:

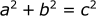
Typically you need to find the length of the hypotenuse:

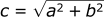
This is all the detail you need to know about Pythagoras' theorem, but we will be using this in the topics coming up.

Sine function

You may recall SOHCAHTOA, which is an acronym to help you remember how each of the sine, cosine, and tangent functions are calculated.

The sine function can be remembered as the opposite side (of the angle) divided by the hypotenuse. The hypotenuse is always the longest side of the triangle, in this case, side c. If you refer to the “SOH” of SOHCAHTOA you can see that:

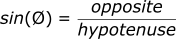
In the case of the picture above:

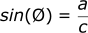
Cosine function

The cosine function works in a similar way to the sine function. The “CAH” of the SOHCAHTOA refers to:

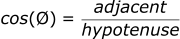
Referring to the diagram:

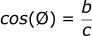
Tangent function

The tangent function is the “TOA” of SOHCAHTOA:

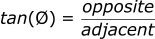
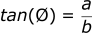
We can use these functions to help us calculate missing variables. If we know the angle and the length of side a or c, we can calculate whichever length we are missing. If we know the lengths of a and c, we can calculate the angle. We will show how this can be implemented when we discuss vectors next.

Vectors

A vector can be simply defined as something with magnitude and direction. If we look at the following images, both have the same magnitude, but different directions:

Vector [1,1]

Vector [-1,1]

Vectors are defined with an x and y coordinate located at the tail of the vector. A 2D vector takes the form of [x,y]. In the first case above, the vector begins at the origin (x=0,y=0) and ends at (x=1,y=1).

Vectors can have any number of dimensions, for example a 3D vector would have the format [x,y,z]. For the purpose of these articles, we will require the ability to break a vector into its components.

For example, let’s assume we have a vector with a magnitude of 10 and it is at a 45 deg angle:

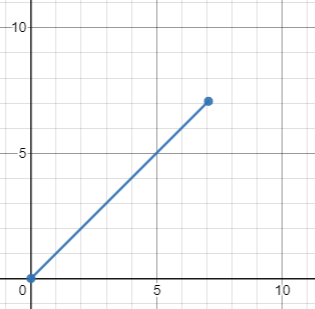Vector magnitude of 10, at a 45 deg angle

If we have a visual of the vector, it is easy to break this down into the x and y components. We can estimate that the vector would be approximately [7,7]

If we want to know the precise answer, we can use the trigonometry we learned in the previous section.

Let’s mark up the diagram above so it looks more familiar:

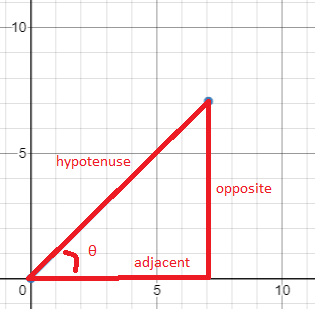
We know that the x axis along the adjacent side of the triangle. If we want to find the x component of the vector, we need to find the length of the adjacent side of the triangle.

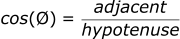
Solving for the adjacent side:

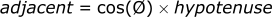
We know that the magnitude is 10 (hypotenuse) and that the angle is 45 deg. We can plug these directly into the function.

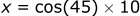
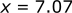
We can do the same thing for the y axis using the sine function:

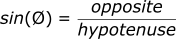
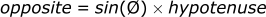
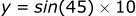
This may feel like a trivial concept, but it will be fundamental in the coming sections when we deal with velocity and acceleration which are both vectors.

The relationship between acceleration, velocity, position

Acceleration, velocity, and position is at the root of calculating a trajectory. Each of these terms are intertwined with each other, it is critically important to understand this section.

Position

Position is described as a location relative to a start point. Position will be measured in meters (m).

Note: A common convention is that the z direction is vertical in the direction of gravity. The x and y directions are perpendicular to the z axis and extend horizontally parallel to the ground. Here is the Cartesian coordinate system which visualizes this convention.

To give a practical example, imagine throwing a ball straight up in the air. We can set the ground as z=0. If the ball reaches 10 m above the ground, z = 10.

Velocity

Velocity can be thought of as the change in position over a period of time. Time is measured in seconds (s). The faster an object changes position, the greater the velocity. Velocity will be measured in meters per second (m/s).

Let’s see how we could calculate the velocity of an object only travelling in the x direction. To start, we will define our terms:

• vx = velocity in x direction (m/s)
• xfinal = final position of object (m)
• xinitial = starting position of object (m)
• tfinal = time when object reaches final position (s)
• tinitial = time immediately before object starts moving (s)

The equation for velocity in the X direction is:

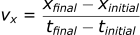
When taking the difference between two times or two positions, this is normally written using the delta symbol.

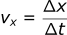
Velocity is a vector, in the case above, that is the equation for velocity in the x direction. What happens if the position changes in both the x and y directions over a period of time?

Here is an example:

A ball is rolled along the ground, it moves 3 meters in the x direction and 2 meters in the y direction in a period of 2 seconds. Assuming it moves at a constant speed for the 2 seconds, what is the absolute velocity of the ball?

First we calculate the velocity in the x direction vx:

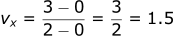
Then we calculate the velocity in the y direction vy:

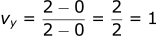
This gives us the velocity vector:

v = [1.5,1]

Which also can be expressed as this triangle:

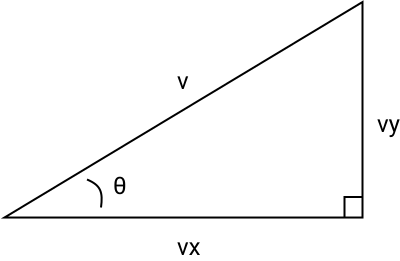
Then to find the absolute velocity, we use Pythagoras' theorem:

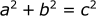
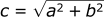
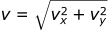
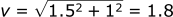
We can also find the angle that the ball is rolled at:

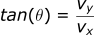
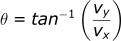
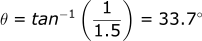
This showcases how the velocity of the ball is a vector with both a magnitude (1.8 m/s) and a direction (33.7 degrees).

Acceleration

Acceleration is the change in velocity over a period of time. Acceleration is measured in meters per seconds squared (m/s²). Here are the terms that act in the x direction:

• ax = acceleration in x direction(m/s²)
• vxfinal = final velocity of object (m/s)
• vxinitial = starting velocity of object (m/s)
• tfinal = time when object reaches final position (s)
• tinitial = time immediately before object starts moving (s)

It can be defined in a similar way to velocity:

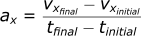
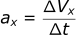
Like velocity, acceleration is also a vector and can have x,y,and z components.

Important Note

These simple equations for velocity and acceleration only apply in specific cases:

• The position or velocity change has to be constant over the period of time
• OR the time interval is very small (which allows for case 1 to be assumed)

In the cases we will discuss going forward, one of these two assumptions will be valid at all times.

Next article: Calculating 1D Trajectory